最小生成树 Minimum Span Tree

有权图 Weight Graph

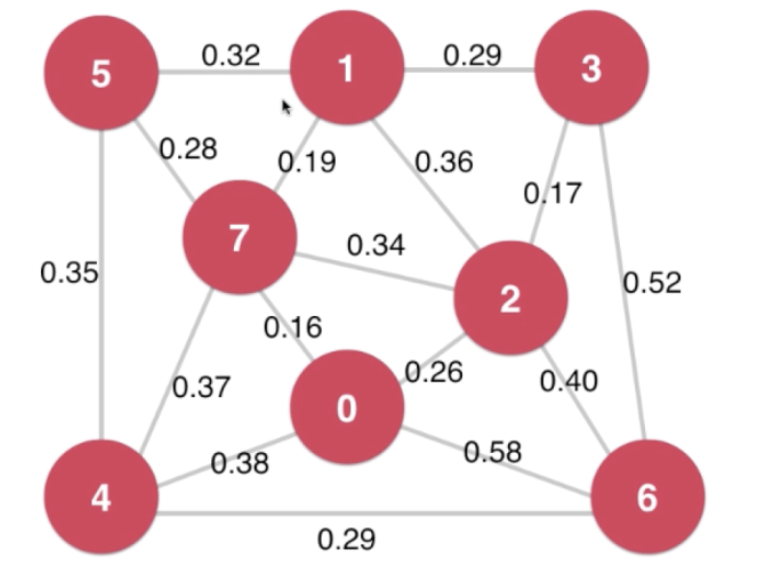
image-20191015113148395

邻接矩阵 Adjacent Matrix

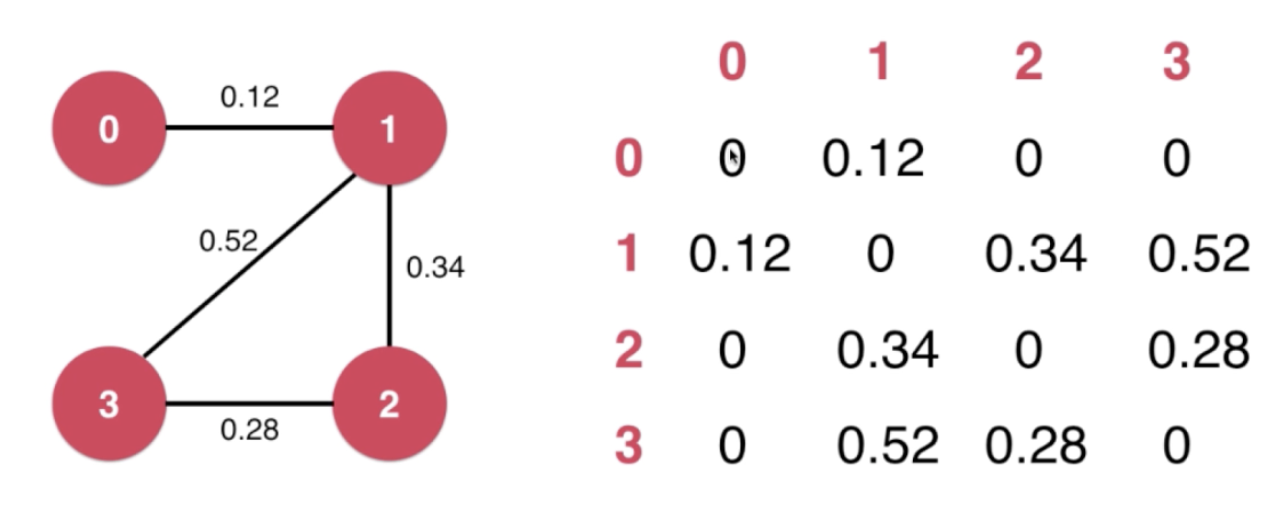
image-20191015113222554

邻接表

image-20191015113341451

使用Edge 表示每一条连接边

最小生成树问题和切分定理

带权无向图、连通图

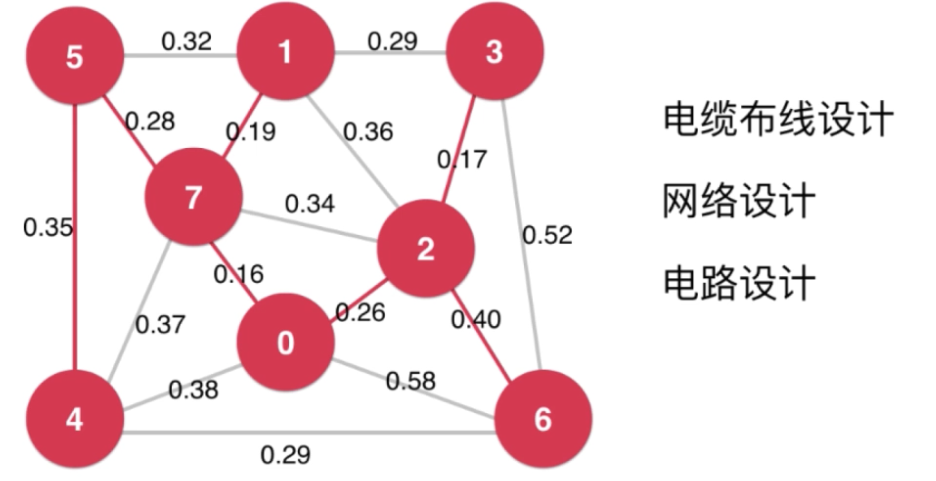
image-20191015212607027

找V-1条边

切分定理 Cut Property

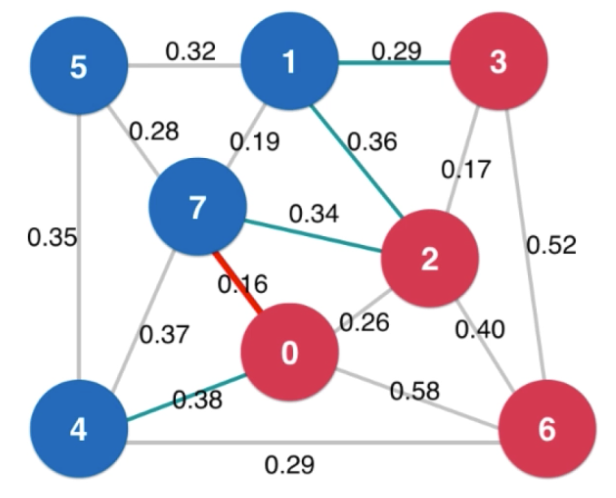
image-20191015213744954

把图中的节点分成两部分，成为一个切分(Cut)

如果一个边的两个端点，属于切分不同的两边，这个边成为横切边(Crossing Edge);

切分定理：

给定任意切分，横切边中权值最小的边必然属于最小生成树

Prim算法 Lazy Prim

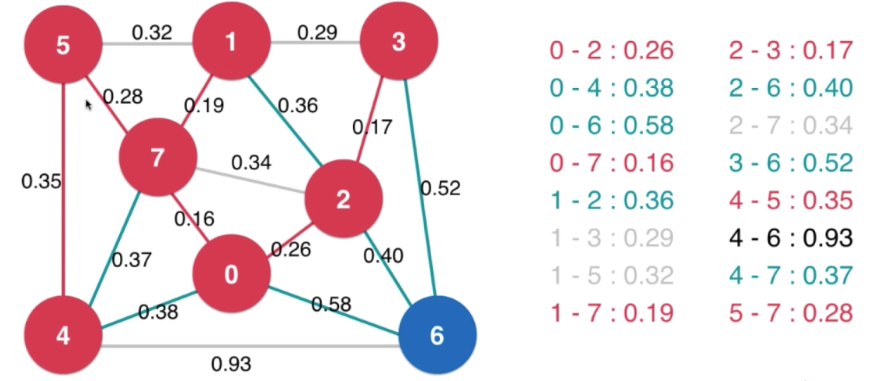
image-20191015214638291

Lazy Prim 最小堆中依然有不会是横切边的边。

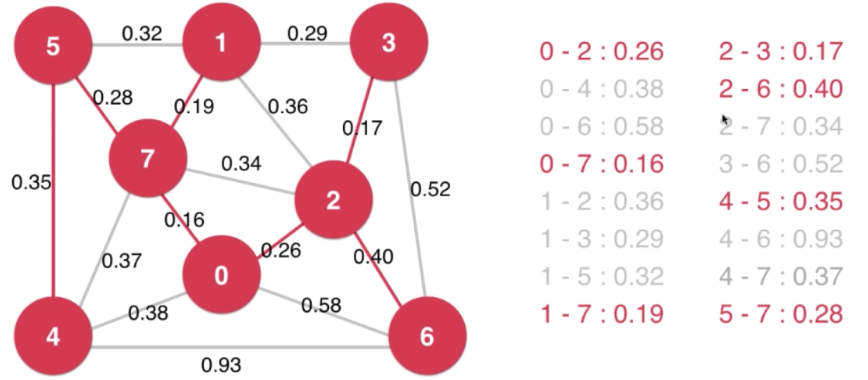
image-20191015214824240

Lazy Prim 的时间复杂度为O(ElogE)

Prim 算法优化

时间复杂度O(ElogV)

IndexMinHeap

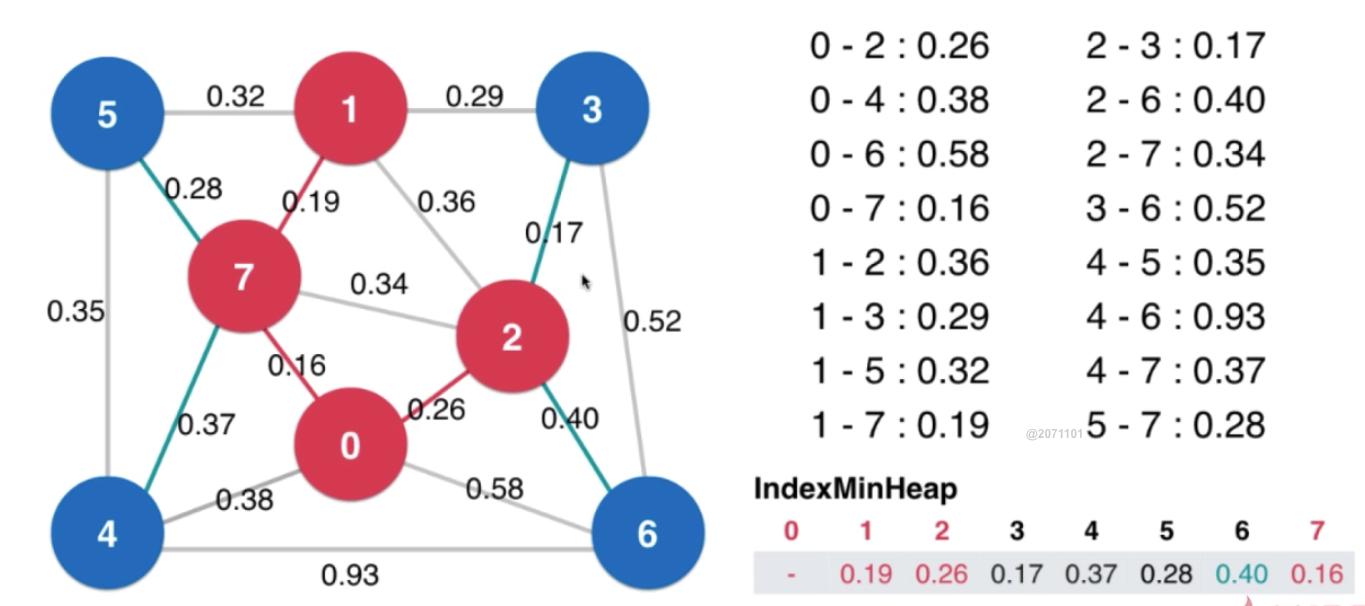
image-20191016094726969

Kruskal算法

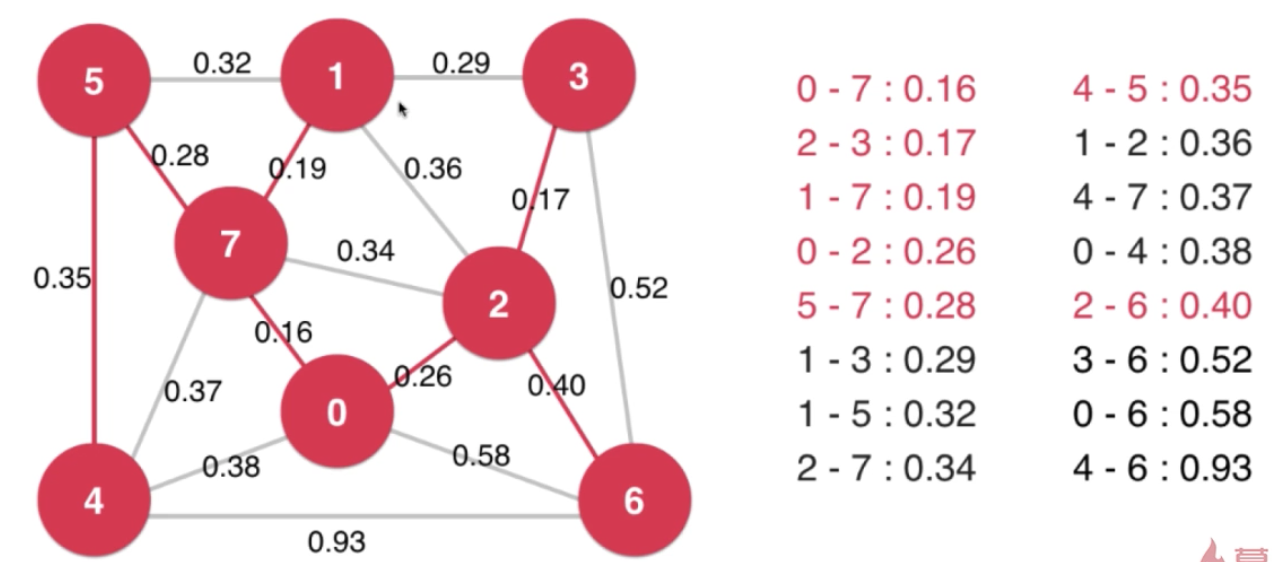
image-20191016095545223

使用并查集

使用Union Find 快速判断环

最小生成树问题

最小生成树问题思考

Lazy Prim O(ElogE)

Prim O(ElogV)

Kruskal O(ElogE)

如果横切边有相等的边

根据具体的算法实现，每次选择一个边

此时，图存在多个最小生成树

Vyssotsky’s Algorithm

将边逐渐添加到生成树中

一旦形成环，删除环中权值最大的边