动态规划基础
什么是动态规划
斐波那契数列 Fibonacci Sequence
1//时间复杂度 应该是指数级
2int fib(){
3 if(n==0){
4 return 0;
5 }
6 if(n==1){
7 return 1;
8 }
9 return fib(n-1)+fib(n-2);
10}
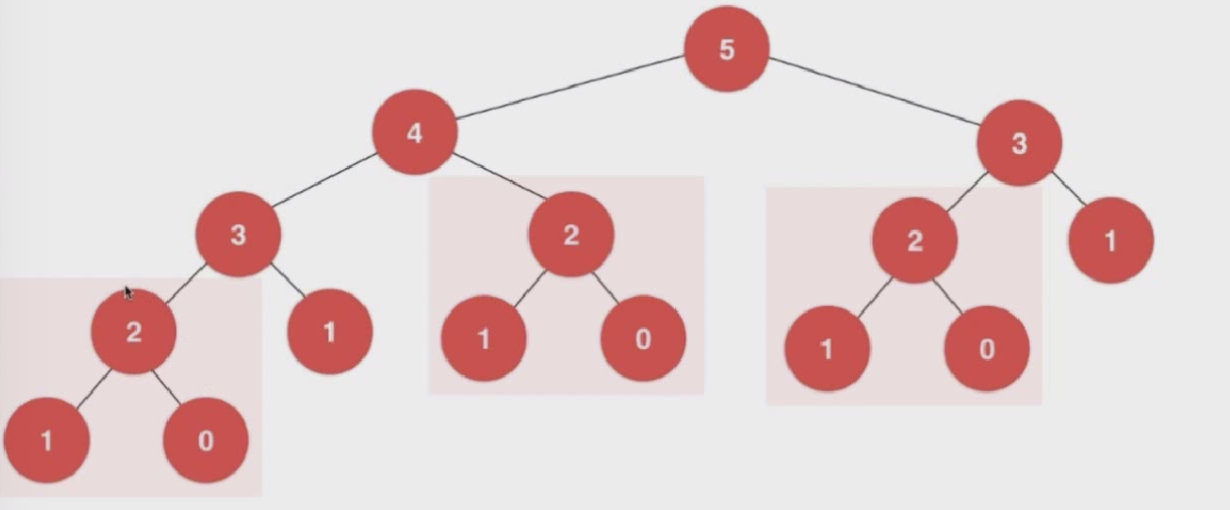
递归会有很多的重复计算,重复的计算量会非常大。
所以想办法对重复的计算 只计算一次
记忆化搜索-自上而下的解决问题
改进的Fibonacci
1// 记忆化搜索 时间复杂度O(n)
2int memo[];
3int fib(){
4 if(n==0){
5 return 0;
6 }
7 if(n==1){
8 return 1;
9 }
10 if(memo[n]==-1){
11 memo[n]=fib(n-1)+fib(n-2);
12 }
13 return memo[n];
14}
动态规划-自下而上的解决问题
1// 动态规划
2int fib(int n){
3 vector<int> memo(n+1, -1);
4 memo[0] = 0;
5 memo[1] = 1;
6 for(int i=2; i<n;i++){
7 memo[i] = memo[i-1]+memo[i-2];
8 }
9 return memo[n];
10}
动态规划:
- 将原问题拆解成若干子问题,同时保存子问题的答案,使得每个子问题值求解一次,最终获得原问题的答案。
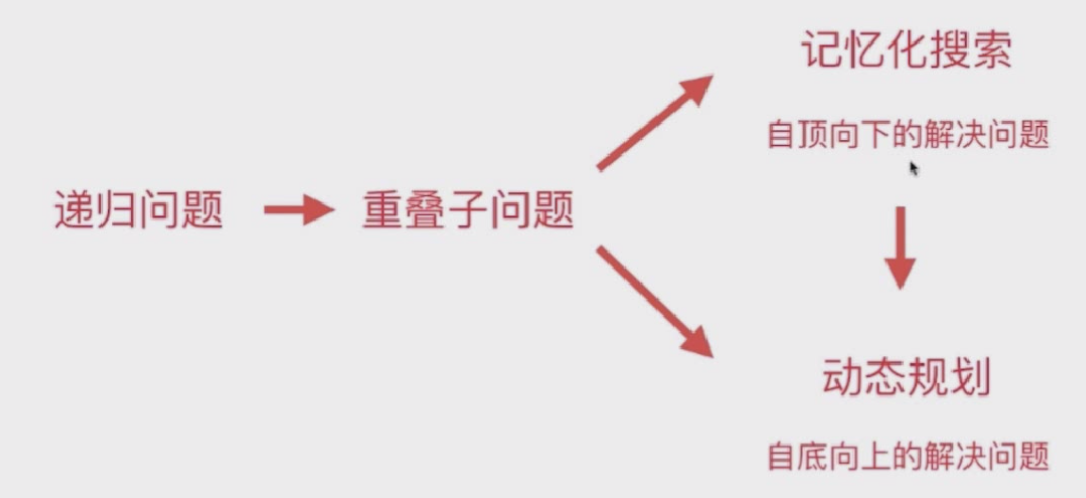
递归问题-> 重叠子问题
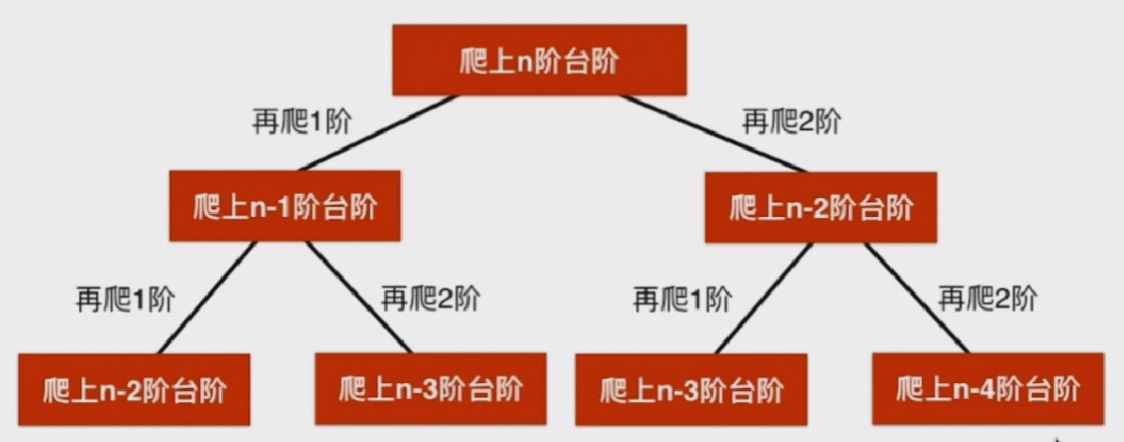
爬楼梯问题