「算法与数据结构」Tree

单链表的查询时间复杂度是O(n)

跳表

树

图

Linked List 是特殊化的Tree

Tree 是特殊化的图

斐波那契，状态树，递归树

状态树空间

决策树空间

二叉树

满二叉树：一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上。

完全二叉树:

存储结构:

链式存储

1// golang
2type Node struct {
3	Data      int64
4	LeftNode  *Node
5	RightNode *Node
6}

// C++ struct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode(int x): val(x), left(NULL), right(NULL){} }

 1
 23. ```java
 3public class TreeNode{
 4  public int val;
 5  public TreeNode left,right;
 6  public TreeNode(int val){
 7		this.val=val;
 8    this.left=NULL;
 9    this.right=NULL;
10  }
11}

数组: 适用于表示完全二叉树，对于稀疏二叉树是非常浪费空间的。

1	Tree := make([]int64,1000)
2	// 一般情况下，0 为root节点。 对于n位置的节点 左孩子 Tree[2*n-1]， 右孩子为Tree[2*n]

中序遍历，前序遍历

 1import java.util.*;
 2
 3public class Solutions {
 4
 5    public class TreeNode {
 6            int val;
 7            TreeNode left;
 8            TreeNode right;
 9            TreeNode(int x) { val = x; }
10         }
11    public TreeNode Solutions(int [] pre,int [] in) {
12        if(pre == null || in == null || pre.length == 0){
13            return null;
14        }
15        int rootValue = pre[0];
16        TreeNode node = new TreeNode(rootValue);
17        for(int i = 0; i < in.length; i++){
18            if(in[i] == rootValue ){
19                if(pre.length > 1){
20                    node.left = Solutions(Arrays.copyOfRange(pre, 1, i+1),
21                                                 Arrays.copyOfRange(in, 0,i));
22                    node.right = Solutions(Arrays.copyOfRange(pre,i+1,pre.length),
23                                                  Arrays.copyOfRange(in,i+1,in.length));
24                }else{
25                    node.left = null;
26                    node.right = null;
27                }
28                
29            }
30        }
31      
32        return node;
33    }
34
35
36    public static void main(String[] args) {
37        int[] a = new int[]{1,2,3,4,5,6,7};
38        int[] b = new int[]{3,2,4,1,6,5,7};
39
40        Solutions solution = new Solutions();
41        TreeNode node = solution.Solutions(a,b);
42        System.out.println("result");
43
44        int i = 0;
45
46        //int s = i++ + i;
47        int tmp = i;
48        i = i +1;
49        i = tmp +i;
50        
51        System.out.println(  (byte)129);
52    }
53}

二叉搜索树

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

定义

二叉排序树或者是一个棵空树，或者具有下列性质的二叉树

若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若右子树不空，则右子树上所有节点的值均大于它的根节点的值；
左、右子树也分别为二叉排序树；
没有键值相等的节点。

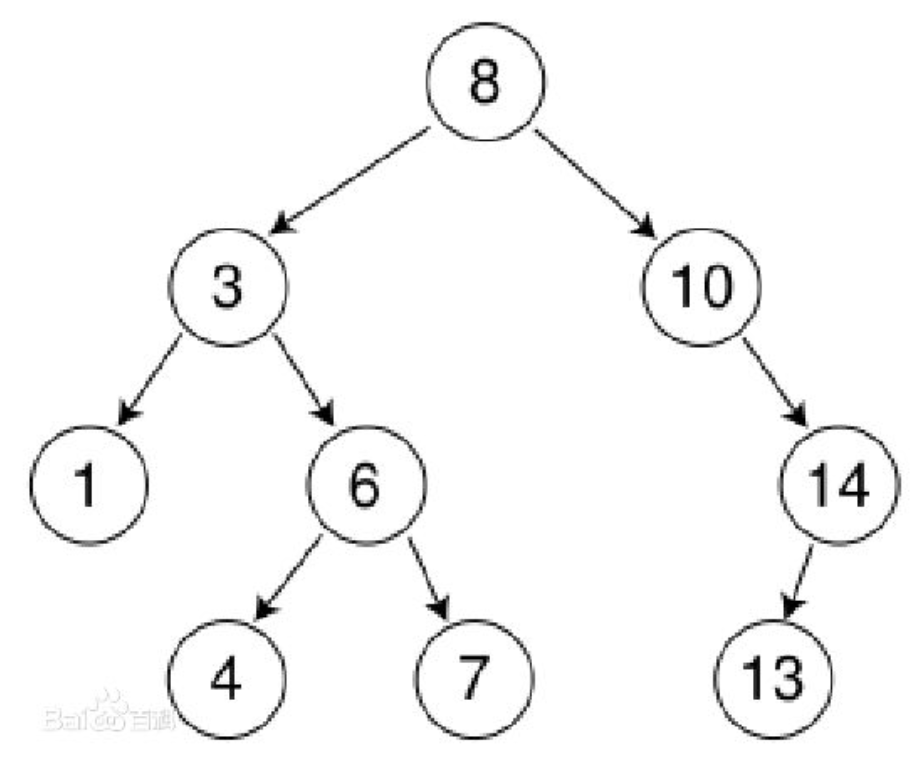
中序遍历：升序排列

左子树始终要小于右子树

查找

时间复杂度：O(logn) 步骤：

若根结点的关键字值等于查找的关键字，成功。
否则，若小于根结点的关键字值，递归查左子树。
若大于根结点的关键字值，递归查右子树。
若子树为空，查找不成功。

插入

首先执行查找算法，找出被插结点的父亲结点。判断被插结点是其父亲结点的左、右儿子。将被插结点作为叶子结点插入。若二叉树为空。则首先单独生成根结点。注意：新插入的结点总是叶子结点。

删除

在二叉排序树删去一个结点，分三种情况讨论：

若*p结点为叶子结点，即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构，则可以直接删除此子结点。
若*p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点*f的左子树（当*p是左子树）或右子树（当*p是右子树）即可，作此修改也不破坏二叉排序树的特性。
若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整，可以有两种做法：其一是令*p的左子树为*f的左/右(依*p是*f的左子树还是右子树而定)子树，*s为*p左子树的最右下的结点，而*p的右子树为*s的右子树；其二是令*p的直接前驱（或直接后继）替代*p，然后再从二叉排序树中删去它的直接前驱（或直接后继）－即让*f的左子树(如果有的话)成为*p左子树的最左下结点(如果有的话)，再让*f成为*p的左右结点的父结点。在二叉排序树上删除一个结点的算法如下：

二叉树顺序存储结构

https://www.jianshu.com/p/74490c570cc1

https://blog.csdn.net/u012469528/article/details/81475824

二叉树的遍历

深度优先遍历（前/中/后序遍历）

1# pre-order In-order Post-order
2
3func() preOrder(root TreeNode){
4	if root != nil{
5		print(root.val)
6		preOrder(root.left)
7		preOrder(root.right)
8	}
9}

递归遍历

 1/**
 2 * Definition for a binary tree node.
 3 * type TreeNode struct {
 4 *     Val int
 5 *     Left *TreeNode
 6 *     Right *TreeNode
 7 * }
 8 */
 9func inorderTraversal(root *TreeNode) []int {
10    
11    tmp := make([]int,0,0)
12    if root == nil{
13        return tmp
14    }
15    if root.Left != nil{
16        tmp = append(tmp,inorderTraversal(root.Left)... )
17    }
18    tmp = append(tmp, root.Val)
19     if root.Right != nil{
20        tmp = append(tmp,inorderTraversal(root.Right)... )
21    }
22    return tmp
23}

非递归遍历

广度优先遍历（层序遍历）

优先队列（最大堆，最小堆）

平衡二叉树

平衡树，即平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用算法有红黑树、AVL、Treap、伸展树、SBT等。

对一棵查找树（search tree）进行查询/新增/删除等动作, 所花的时间与树的高度h 成比例, 并不与树的容量 n 成比例。如果可以让树维持矮矮胖胖的好身材, 也就是让h维持在O(lg n)左右, 完成上述工作就很省时间。能够一直维持好身材, 不因新增删除而长歪的搜寻树, 叫做balanced search tree（平衡树）。平衡树有很多种, 其中有几类树维持平衡的方法。

Airren Ren